روش دالامبر، یکی از نوآورانهترین و تأثیرگذارترین شیوههای حل معادلات دیفرانسیل به شمار میرود که در قرن هجدهم توسط ریاضیدان شهیر فرانسوی، ژان دالامبر، ارائه شد. این روش نه تنها به عنوان ابزاری سودمند در پژوهشهای علمی و مهندسی، بلکه به عنوان پلی برای درک عمیقتر مفاهیم ریاضیاتی و فیزیکی، به کار گرفته شده است. دالامبر با تکیه بر اصول منطقی و تجریبات ریاضی، روشی را بنیان نهاد که همچنان در دنیای امروز و در محافل علمی پیشرفته مورد توجه قرار دارد. در این مقاله، به بررسی اجمالی این روش و کاربردهای آن در زمینههای مختلف علمی خواهیم پرداخت.
مقدمه
- روش دالامبر و تأثیر آن بر دقت محاسبات ریاضی
- چالشها و جذابیتهای الگوهای هندسی در دالامبر
- پیشنهاداتی برای بهبود فهم روش دالامبر در آموزش
- کاربردهای عملی روش دالامبر در حل معادلات و مسائل روزمره
- سوال و جواب
- In Retrospect

روش دالامبر و تأثیر آن بر دقت محاسبات ریاضی
روش دالامبر که به عنوان یک روش عددی برای حل معادلات و محاسبات ریاضی مطرح شده است، تأثیر شگرفی در دقت محاسبات دارد. این روش به دلیل قابلیت تفکیک و به کارگیری پلهای، به ما امکان میدهد تا با کاهش خطاها و به حداقل رساندن تخمینها، محاسبات را به دقت بیشتری انجام دهیم. برای نمونه، در حل معادلات چندجملهای، این روش به ما کمک میکند تا با استفاده از تحلیل دقیق نقاط تقاطع، نتایج نزدیکتری به حقیقت بدست آوریم.
به کارگیری این روش در محاسبات عددی، مزایای فراوانی به همراه دارد که میتوان به موارد زیر اشاره کرد:
- کاهش خطای تقریبی: با تفکیک محاسبات به مراحل کوچکتر، دقت نتایج بیشتر میشود.
- تسهیل در حل معادلات: قابلیت پایهگذاری حلها بهترتیب منطقی، کارایی را افزایش میدهد.
- انعطافپذیری: قدرت تطبیق با انواع مختلف معادلات و شرایط ویژه، از ویژگیهای این روش است.
| ویژگی | تأثیر بر دقت |
|---|---|
| تحلیل دالامبر | افزایش قابل توجه دقت در محاسبات |
| کاهش خطا | حداقل کردن اشتباهات رایج |
در نهایت، روش دالامبر نه تنها به عنوان یک ابزار لحظهای در محاسبات ریاضی مطرح است، بلکه بهعنوان یک بنیان در نظریههای عددی و کاربردهای علمی نیز شناخته میشود. با ورود به دنیای فناوری و علم داده، استفاده از این روش قادر به ویرایش و بهبود دقت محاسبات در پروژههای مختلف خواهد بود. برای اطلاعات بیشتر میتوانید به این لینک مراجعه کنید.
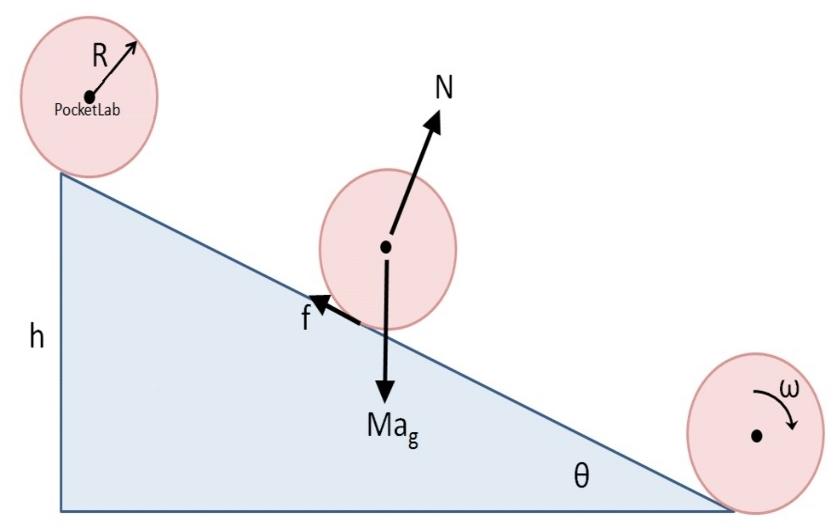
چالشها و جذابیتهای الگوهای هندسی در دالامبر
الگوهای هندسی در دالامبر یک دنیای وسیع و جذاب هستند که چالشهای خاصی را به همراه دارند. برنامهنویسان و پژوهشگران اغلب با دغدغههایی مواجه میشوند که نیاز به نوآوری و خلاقیت دارند. از جمله این چالشها میتوان به موارد زیر اشاره کرد:
- پیچیدگی محاسباتی: درک و پیادهسازی این الگوها میتواند زمانبر باشد.
- نیاز به دقت بالا: هر تغییر کوچک در پارامترها میتواند نتیجه را دگرگون کند.
- مدیریت منابع: شبیهسازیهای هندسی معمولاً به منابع محاسباتی بالایی نیاز دارند.
با وجود این چالشها، الگوهای هندسی دالامبر جذابیتهای خاصی را نیز به همراه دارند که آنها را از سایر روشها متمایز میکند. این جذابیتها شامل:
- زیبایی بصری: نتایج تولید شده غالباً فراتر از تصور هستند.
- کاربردهای جذاب: این الگوها در طراحی، هنر و ریاضیات به کار میروند.
- نوآوری در حل مسائل: استفاده از این الگوها میتواند راهکاری جدید و خلاقانه برای مسائل سنتی باشد.
| چالشها | جذابیتها |
|---|---|
| پیچیدگی محاسباتی | زیبایی بصری |
| نیاز به دقت بالا | کاربردهای جذاب |
| مدیریت منابع | نوآوری در حل مسائل |
برای کسب اطلاعات بیشتر درباره روش دالامبر و کاربردهای آن، میتوانید به این لینک مراجعه کنید.
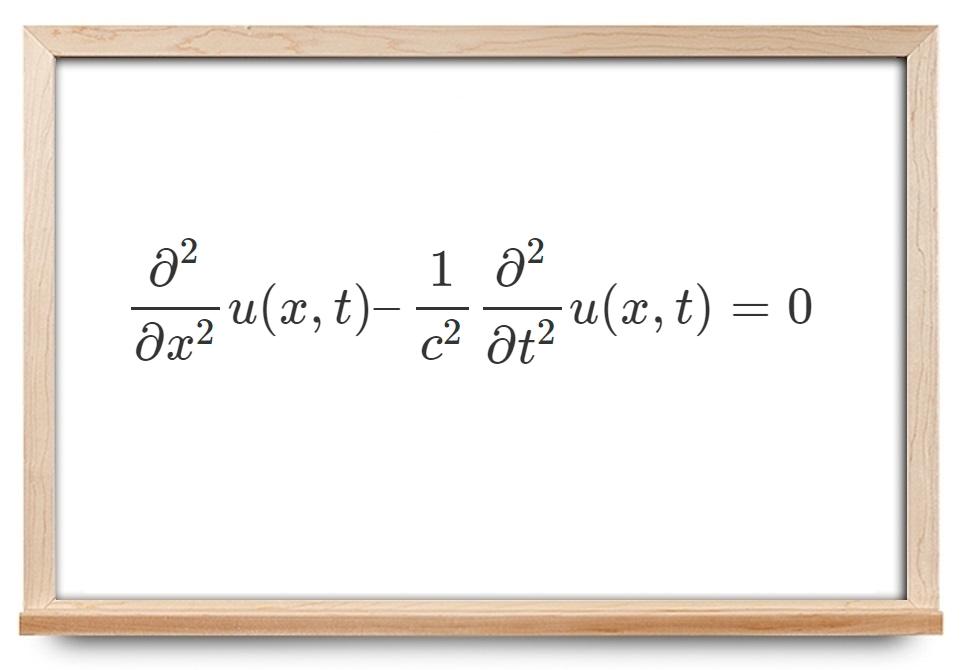
پیشنهاداتی برای بهبود فهم روش دالامبر در آموزش
برای بهبود فهم روش دالامبر در آموزش، گامهای ماندگاری را باید در نظر گرفت. نخست، تمرکز بر آموزش عملی و تجربی میتواند اثربخشی این روش را افزایش دهد. به عنوان مثال، استفاده از پروژههای گروهی و فعالیتهای عملی به دانشآموزان کمک میکند تا مفاهیم را بهصورت عمیقتری درک کنند. علاوه بر این، استفاده از ابزارهای بصری و تکنولوژیهای نوین مانند اپلیکیشنهای تعاملی، میتواند جذابیت این روش را بیشتر کند و تعامل دانشآموزان را افزایش دهد.
در مرحله دوم، فراهم آوردن فرصتهای بحث و تبادل نظر در کلاس میتواند به فهم بهتر این روش کمک شایانی نماید. برگزاری جلسات پرسش و پاسخ و استفاده از فرمتهای گروهی برای مباحثه در مورد موضوعات مختلف دالامبر، میتواند فضای یادگیری را عمیقتر کند. به طور کلی، ایجاد یک محیط یادگیری پویا که در آن دانشآموزان به تبادل دیدگاهها پرداخته و از تجربیات یکدیگر بهرهبرداری کنند، میتواند کلید موفقیت در کاربرد این روش باشد.

کاربردهای عملی روش دالامبر در حل معادلات و مسائل روزمره
روش دالامبر به عنوان یک ابزار ریاضی با قابلیتهای منحصر به فرد خود، در حل مسائل متنوع و چالشهای روزمره مورد استفاده قرار میگیرد. این روش با بهرهگیری از اصول جبر و تحلیل عددی، امکان یافتن راهحلهای تقریبی برای معادلات غیرخطی را فراهم میآورد. در زیر به چندین کاربرد عملی این روش اشاره میشود:
- تحلیل سیستمهای دینامیکی: در مواردی همچون تحلیل حرکات روانه و دینامیکی خودروها و سازهها.
- مدلسازی مالی: برای پیشبینی عملکردهای بازار سرمایه و تحلیل ریسکهای مالی.
- پزشکی: در شبیهسازی و تحلیل دادههای بیولوژیکی و پزشکی برای تشخیص دقیقتر.
این تکنیک علاوه بر کاربردهای خاص، به حل مسائل پیچیده روزمره نیز کمک میکند. بهعنوان مثال، در طراحی سایتها و بهینهسازی تجربه کاربری، روش دالامبر میتواند به ایجاد الگوریتمهای بهتر و کارآمدتر کمک کند. در جدول زیر، چندین مثال دیگر از این کاربردها مشاهده میشود:
| حوزه | کاربرد |
|---|---|
| علوم کامپیوتر | بهینهسازی الگوریتمها |
| فیزیک | تحلیل نیروها و حرکت اجسام |
| آمار | مدلسازی و پیشبینی دادهها |
استفاده از این تکنیک نه تنها توانمندیهای فرد در حل مسائل را افزایش میدهد، بلکه موجب بهبود کارآیی و دقت در عملکردهای روزمره خواهد شد. برای آشنایی بیشتر با روش دالامبر، پیشنهاد میشود به وبسایت BetReward مراجعه کنید.
سوال و جواب
سوال و پاسخ درباره “روش دالامبر”
سوال ۱: روش دالامبر چیست و در کجا استفاده میشود؟
جواب: روش دالامبر، که به نام ریاضیدان فرانسوی، ژان دالامبر نامگذاری شده است، یک تکنیک عددی برای حل معادلات دیفرانسیل است. این روش به ویژه در مهندسی و علوم کاربردی مورد استفاده قرار میگیرد و به محاسبات دقیق و مدلسازی سیستمها کمک میکند.
سوال ۲: چه زمانی باید از روش دالامبر استفاده کنیم؟
جواب: این روش زمانی مفید است که به دنبال حل معادلات دیفرانسیل و پیادهسازی آن در مسئلهای خاص هستید. بهویژه در مواردی که شرایط مرزی یا اولیه در معادلات وجود دارد، روش دالامبر میتواند راهحلهای بهتری ارائه دهد.
سوال ۳: آیا مزایای خاصی برای استفاده از روش دالامبر وجود دارد؟
جواب: بله، یکی از مزایای اصلی این روش، سادگی آن در پیادهسازی است. همچنین، دقت بالای آن در حل معادلات پیچیده و تطابق منطقی با شرایط واقعی، آن را به ابزاری بسیار قدرتمند در دست محققان و مهندسان تبدیل کرده است.
سوال ۴: معایب روش دالامبر چیست؟
جواب: هرچند روش دالامبر مزایای زیادی دارد، اما ممکن است در برخی مواقع دقیقی که در مقایسه با روشهای دیگر بهدست میآورد، کمتر باشد. همچنین، احتیاج به دقت مشخصات ورودی و شرایط خاص برای عملکرد بهینه آن وجود دارد.
سوال ۵: آیا میتوان روش دالامبر را برای حل مسائل ریاضی دیگر نیز استفاده کرد؟
جواب: بله، این روش میتواند به تناسب برای حل مشکلات مختلفی در ریاضیات و فیزیک، و همچنین در زمینههایی مانند اقتصاد و بیوانفورماتیک قابل استفاده باشد. تطبیقپذیری این روش یکی از نکات قوت آن است.
سوال ۶: چگونه میتوان به یادگیری بهتر روش دالامبر پرداخت؟
جواب: برای یادگیری این روش، ابتدا باید با مفاهیم پایهای معادلات دیفرانسیل آشنا شوید. سپس با مطالعه منابع معتبر و انجام تمارین متنوع، میتوانید تسلط خود را بر این روش افزایش دهید. همچنین، تجربیات عملی در پیادهسازی آن در پروژههای مختلف بسیار کمککننده خواهد بود.
سوال ۷: آیا منابعی برای مطالعه بیشتر درباره روش دالامبر وجود دارد؟
جواب: بله، کتابهای تخصصی در زمینه ریاضیات کاربردی و معادلات دیفرانسیل، مقالات علمی و دورههای آموزشی آنلاین موجود هستند که به شما کمک میکنند تا بستر شناخت بهتری از روش دالامبر پیدا کنید. همچنین، گروههای بحث و تالارهای گفتگو میتوانند مکانهای مناسبی برای تبادل نظر و یادگیری باشند.
In Retrospect
در پایان، روش دالامبر به عنوان یک ابزار کلیدی در تحلیل و درک مسائل ریاضی و علمی قابل توجه است. این روش با سادگی و کارآمدی خود، در بسیاری از زمینهها از جمله مهندسی، فیزیک و اقتصاد مورد استفاده قرار میگیرد. با درک دقیقتر این روش و کاربردهای آن، میتوانیم گامهای موثرتری در حل مسائل پیچیده برداریم. امید است که این مقاله به درک عمیقتری از روش دالامبر کمک کرده باشد و الهامبخش خوانندگان برای کاوش بیشتر در دنیای ریاضی و کاربردهای آن باشد.